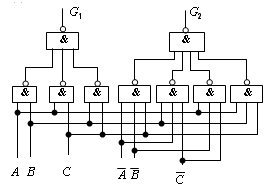
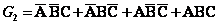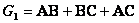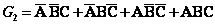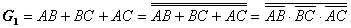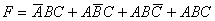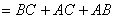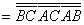例1. 某工厂有A、B、C三个车间和一个自备电站，站内有两台发电机G1和G2。G1的容量是G2的两倍。如果一个车间开工，只需G2运行即可满足要求；如果两个车间开工，只需G1运行；如果三个车间同时开工，则G1和 G2均需运行。试画出控制G1和 G2运行的逻辑图，用与非门实现。
（2） 由逻辑状态表写出逻辑式
例2：设计三人表决电路（A、B、C）。每人一个按键，如果同意则按下，不同意则不按。结果用指示灯表示，多数同意时指示灯亮，否则不亮。要求用与非门实现。
（2） 由状态表写出逻辑式并化简、转换
解：（1） 根据逻辑要求写出逻辑状态表
首先假设逻辑变量取“0”、“1”的含义。
设：A、B、C分别表示三个车间的开工状态：
开工为“1”，不开工为“0”；
G1和 G2运行为“1”，不运行为“0”。
逻辑状态表
| A | B | C | G1 | G2 |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 1 | 1 |
根据状态表写表达式的一般步骤：①在状态表上找出输出为1的行；②将这一行中所有自变量写成乘积项，当变量的取值为“1”时写为原变量，当变量的取值为“0”时写为原变量的反变量；③将所有乘积项逻辑加，便得到逻辑函数表达式。
这里的乘积项又叫最小项，在最小项里，每个变量都以它的原变量或反变量的形式在乘积项中出现，且仅出现一次。
（3） 化简逻辑式
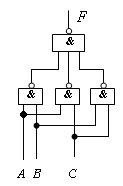
（4） 用“与非”门构成逻辑电路
（5）画出逻辑电路图
解：（1） 根据逻辑要求列状态表
首先确定逻辑变量取0、1的含义：A、B、C分别表示三人按键的状态，键按下时为“1”，不按时为“0”。 F表示指示灯的亮灭，灯亮为“1”， 不亮为“0”。
逻辑要求：两个人（包括两个人）以上同意，指示灯亮。
| A | B | C | F |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 |
（3）实现电路
