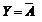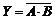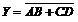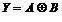逻辑门电路，是指具有多个输入端和一个输出端的开关电路。
根据真值表可得“或非”门的逻辑功能为“全0出1，有1出0”。
一、与门电路
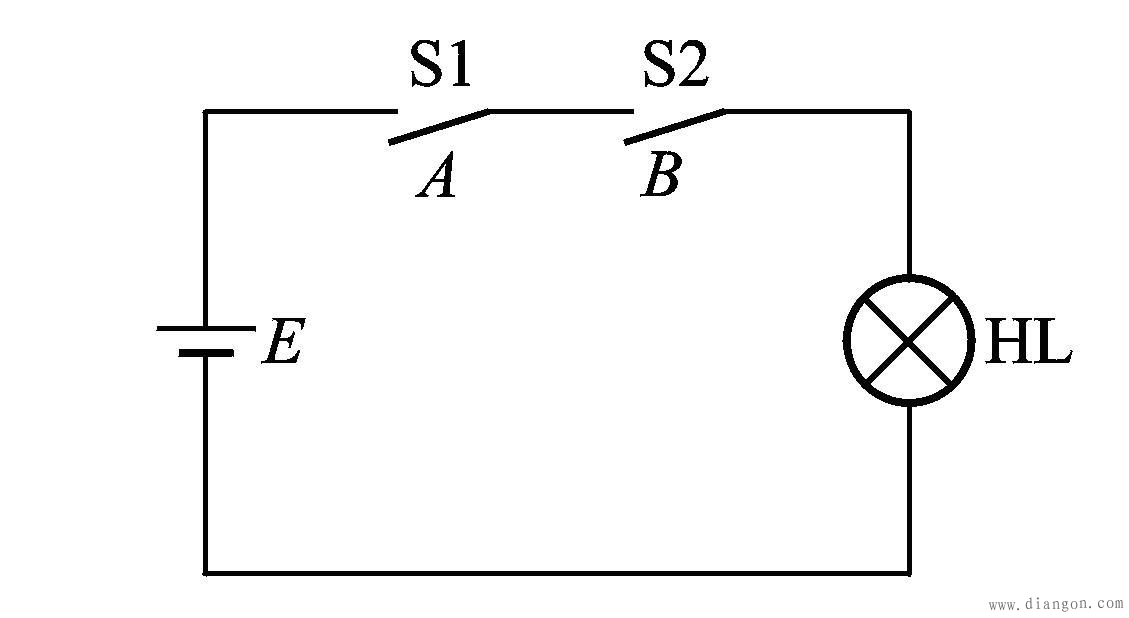
1．实验电路
开关S1、S2都闭合，HL才亮，即使有一个开关断开，灯就灭了。
2．与逻辑
当一件事情的几个条件全部具备之后，这件事情才能发生，否则不能发生。
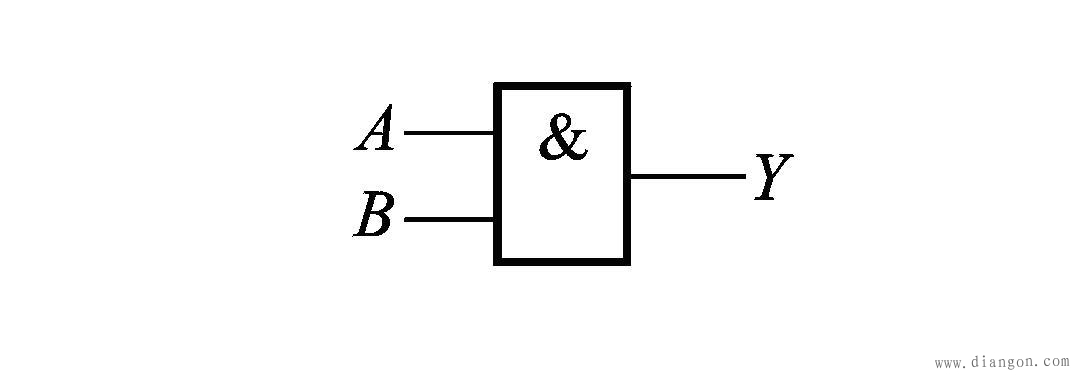
3．逻辑符号
4．函数式
仅当A和B皆为逻辑1时，Y才为1，只要A、B有一个为0、Y即为0，这与逻辑运算的乘法类似，故称逻辑“与”。其逻辑函数式为Y = A×B
5．真值表
A |
B |
Y |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
“与”门电路的逻辑功能是“有0出0，全1出1”。
二、或门电路
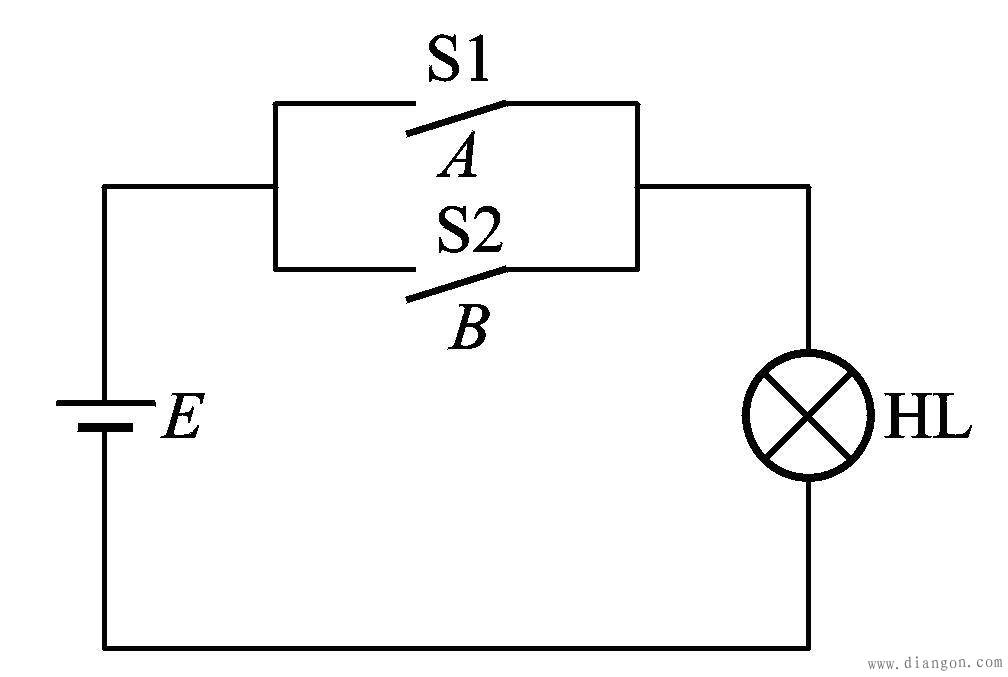
1．实验电路
两个开关中只要有一个闭合，HL就被点亮。
2．或逻辑
即在决定一件事情的各种条件中，只要具备一个条件，这件事情就会发生。这样的因果关系称为“或”逻辑关系。
3．逻辑符号
4．函数式
仅当A和B皆为逻辑0时，Y才为0，只要有一个为1、Y即为1，这与逻辑运算的加法相类似，故称为逻辑加。逻辑加可用代数式表示，其逻辑函数式为Y = A + B
5．真值表
A |
B |
Y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
“或”门的逻辑功能是“有1出1，全0出0”
三、非门电路
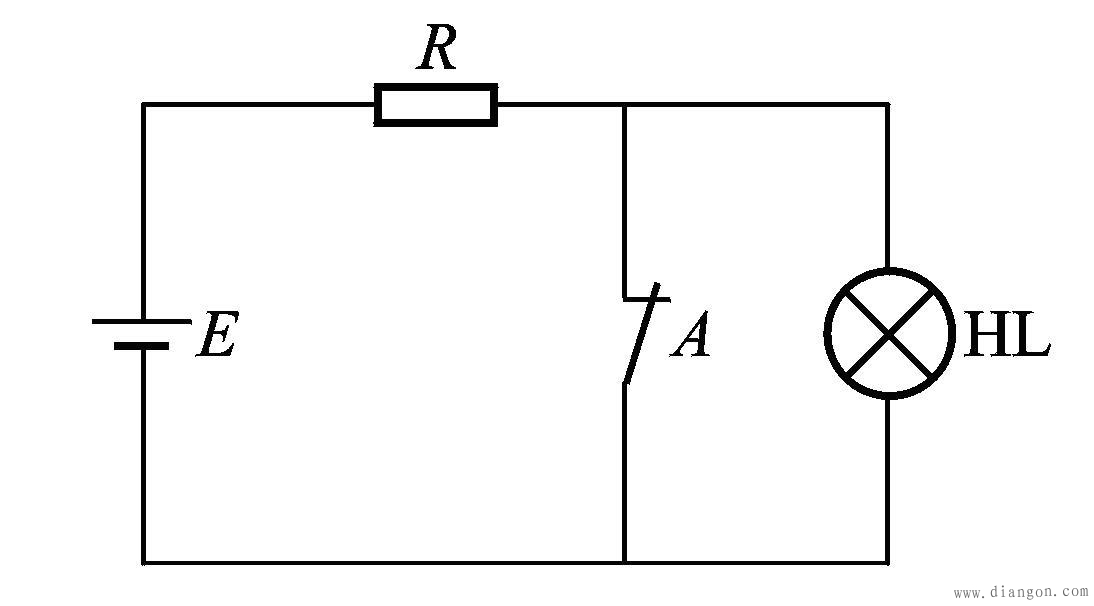
1．实验电路
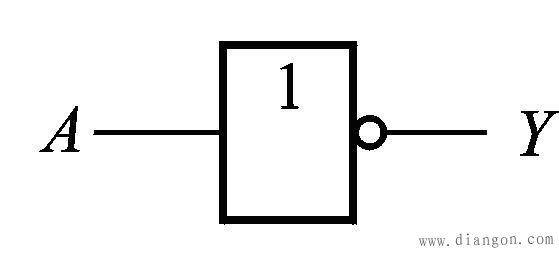
2．逻辑符号
3．表达式
4．真值表
A |
Y |
0 |
1 |
1 |
0 |
“非”门的逻辑功能为“有0出1，有1出0”
四、复合逻辑门电路
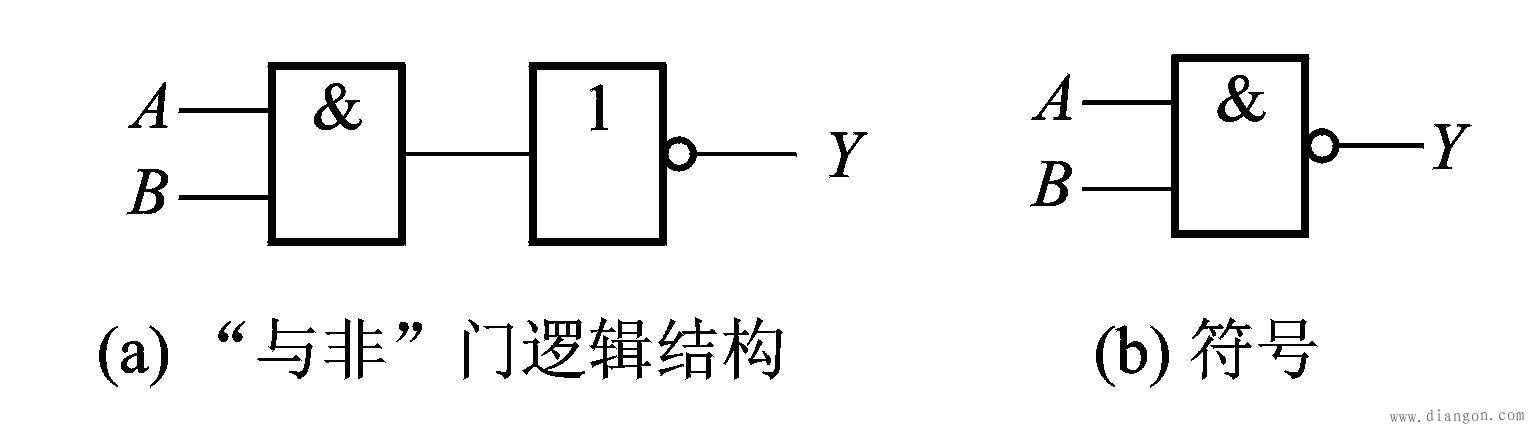
1、与非门电路
将一个与门和一个非门连接起来，就构成了一个“与非”门。
其逻辑函数式 
真值表：
A |
B |
AB | |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
根据真值表可得“与非”门的逻辑功能为“全1出0，有0出1”。
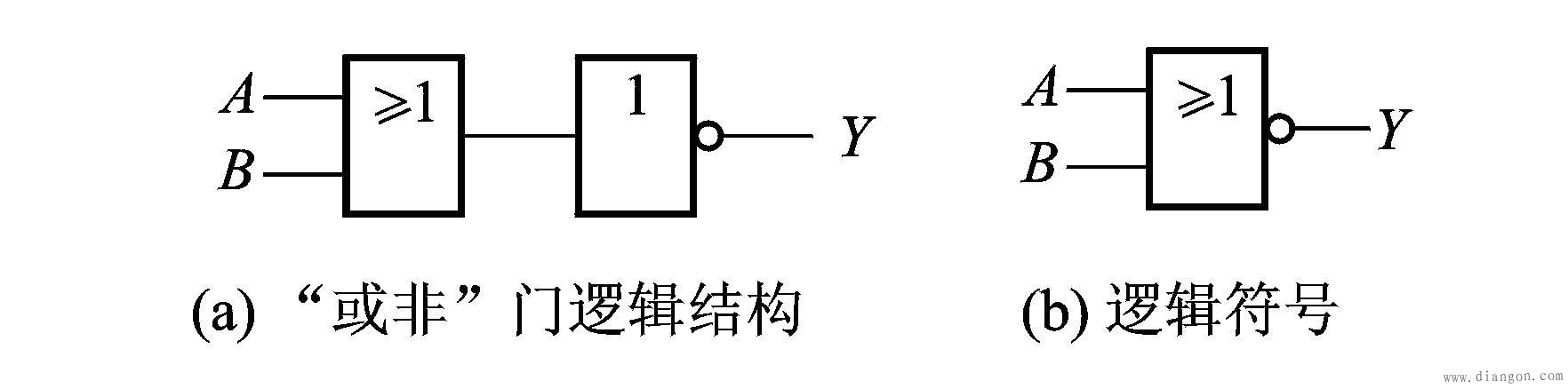
2、或非门电路
在“或”门后面接一个“非”门，就构成“或非”门。
其逻辑函数式
真值表：
A |
B |
A+B | |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
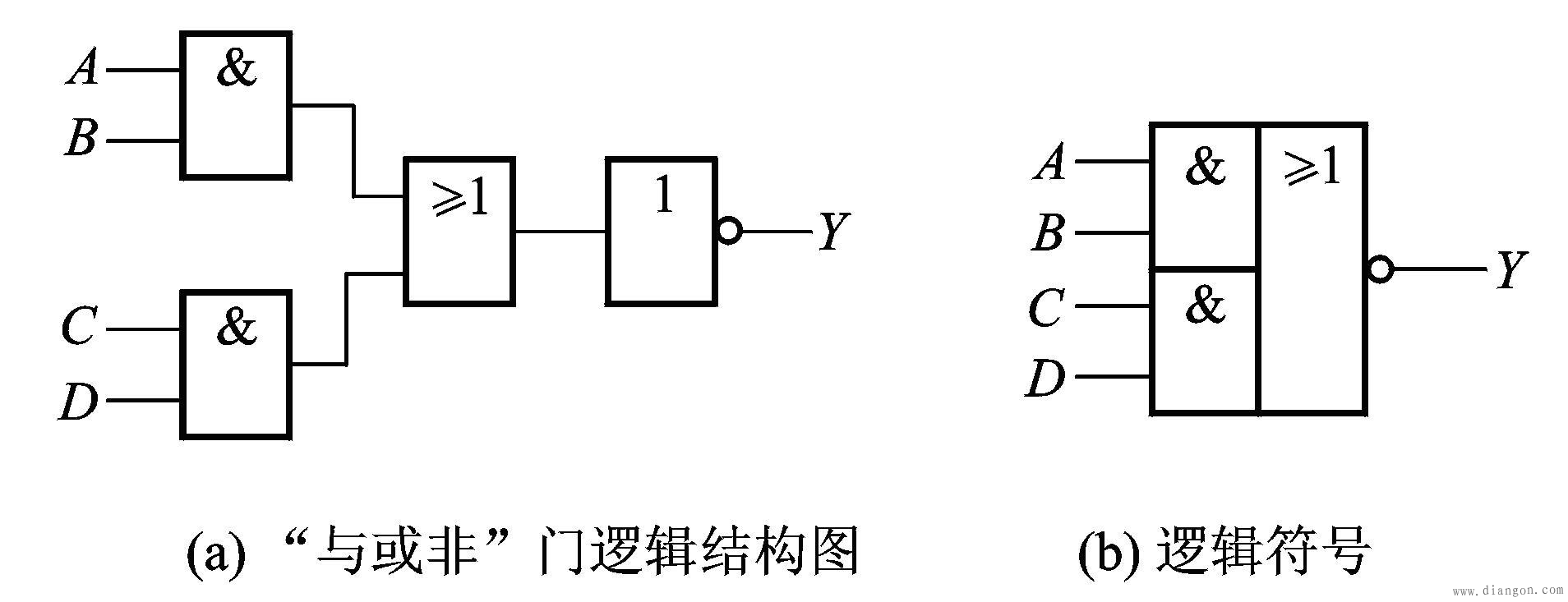
3、与或非门电路
由两个或多个“与”门和一个“或”门，再加一个“非”门串联而成。
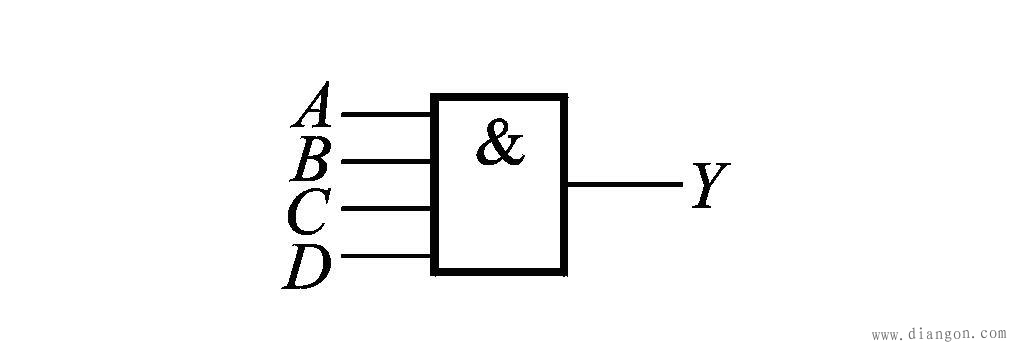
（1）“与或非”门逻辑结构图、逻辑符号
（2）“与或非”门的逻辑关系是：输入端分别先“与”，然后再“或”，最后是“非”。
（3）逻辑函数表达式 
（4）真值表
A |
B |
C |
D |
Y |
A |
B |
C |
D |
Y |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
（5）逻辑功能是：
当输入端任何一组全为1时，输出即为0，只有各组至少有一个为0时，输出才是1。
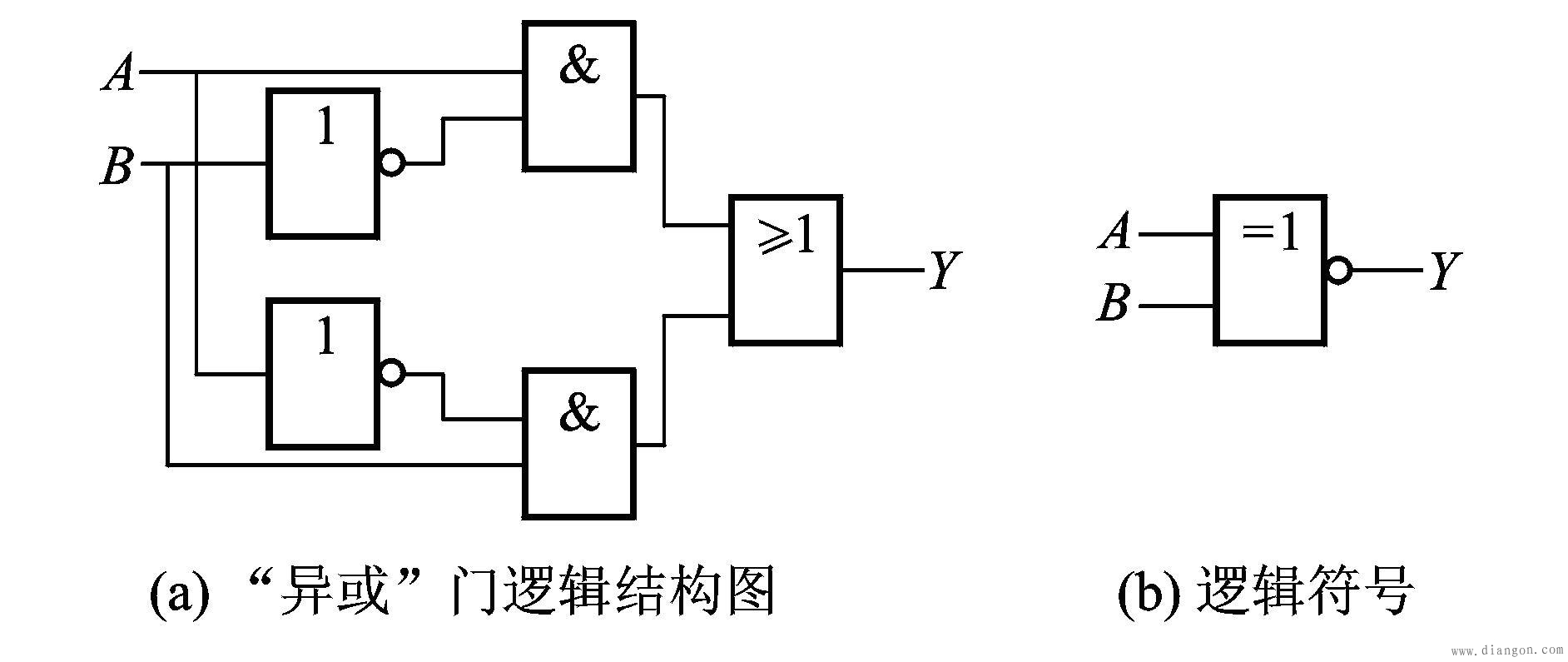
4．异或逻辑门电路
（1）“异或”门逻辑结构图、逻辑符号
（2）真值表
A |
B |
Y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
（3）逻辑函数式
或
或
（4）逻辑功能：当两个输入端一个为0，另一个为1时，输出为1；而两个输入端均为0或均为1时，输出为0。即为“同出0，异出1”。
