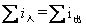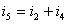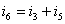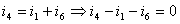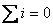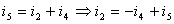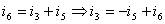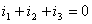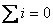描述结点处电流间的约束关系。
对结点a：（注意首先要标明参考方向）在结点a有三个电流与它关联，根据KCL可写出：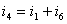 
根据前面的分析我们得到了3个单个结点a，b，c的KCL方程，分别为：
1.定律内容：
在任一时刻，对任一结点，流入结点的电流之和恒等于流出该结点的电流之和。即
如图所示:
对结点b：
对结点c：
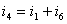
由结点a的KCL方程：
我们可以得到基尔霍夫电流定律的另一种描述：
对任一结点，结点电流代数和等于零，即
。
注意：存在“＋－”号问题，若规定流入结点电流为＋，则流出为－；若规定流出为＋，则流入为－。
KCL实质上反映了支路电流间的关系，揭示了在任一结点上电荷的守恒，即电荷在结点上既没有消失，也没有积累。
2.广义KCL
KCL不仅适用于单个结点，也可推广应用于一个闭合面（又称广义结点）。
对图中的虚线所示闭合面，共有3条支路与其相连，对应的支路电流分别为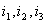
，我们看其是否符合KCL定律。
结点a： 
结点b： 
结点c： 
由上述3个方程，我们可以得出：
可见，对于图中虚线所示的闭合面，如果把它看作一个结点（广义结点），它也满足KCL定律，和它相连的3条支路的支路电流的代数和为0。
描述：任一时刻，通过任意一个封闭面的电流的代数和等于零。
即：这个封闭面可以看成是一个广义大结点，有
。
